Le protocole DPS implique deux acteurs principaux : Alice et Bob, qui jouent des rôles différents. Vous pouvez ici explorer l'ensemble des étapes que chacun d'eux doit suivre pour mener à bien le protocole.
Pour chaque photon à envoyer, générez une séquence aléatoire de 3 bits (b₀, b₁, b₂). Ces bits serviront à encoder l'information sous forme de phase dans le train d'impulsions associé à ce photon.
Générez un train d’impulsions en faisant circuler le photon dans un dispositif à 3 trajets.
Appliquer un déphasage de π dont le bit correspondant est 1.
Attendez la réponse de Bob : il vous communique le temps de détection pour chaque photon (T0, T1, T2 ou T3).
Construisez votre clé : Ignorez les photons détectés à T0 et T3. Pour T1 : si b₀ = b₁, le bit de clé est 0 ; sinon, le bit est 1. Pour T2 : si b₁ = b₂, le bit de clé est 0 ; sinon, le bit est 1.
Chiffrez et envoyez votre message à Bob en utilisant la clé obtenue.
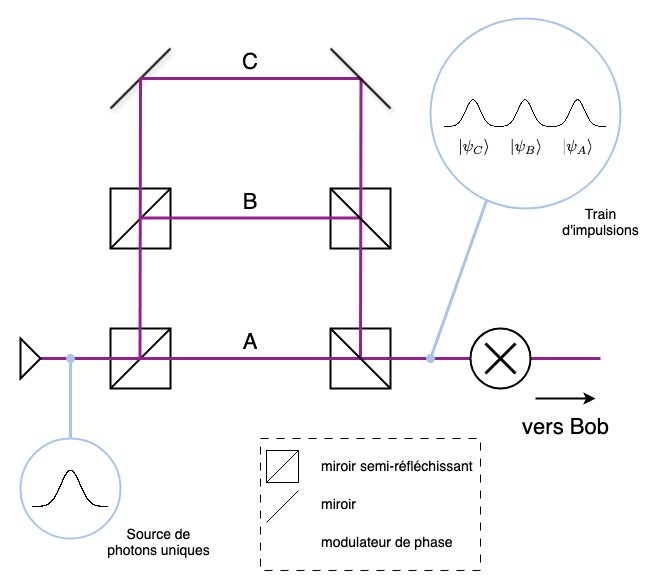
ou, de façon équivalente
\[ \lvert \psi \rangle = \frac{1}{\sqrt{3}}\left( \lvert 0 \rangle + \lvert 1 \rangle + \lvert 2 \rangle \right), \]avec \( \left| 0 \right\rangle \) qui correspond à la 1ere impulsion, \( \left| 1 \right\rangle \) à la seconde impulsion, et \( \left| 2 \right\rangle \) à la dernière impulsion du train. Pour chaque photon envoyé, Alice choisit 3 bits de façon aléatoire. Si le bit est 1, elle applique un déphasage de π à l'impulsion correspondante et elle ne fait rien si le bit est 0. Pour les trois impulsions il y a 8 situations possibles, voyons quatre exemples
| bit 2 | bit 1 | bit 0 | Impulsion 2 | Impulsion 1 | Impulsion 0 |
|---|---|---|---|---|---|
| 0 | 0 | 0 |  |  |  |
| 0 | 1 | 0 |  |  |  |
| 1 | 1 | 0 |  |  |  |
| 1 | 1 | 1 |  |  |  |
On remarque que \( (-1)^0 = 1 \) et \( (-1)^1 = -1, \) on peut donc écrire l'état du photon à l'aide des bits b0, b1 et b2 de la manière suivante
\[ \left| \psi_{\text{photon}} \right\rangle = \frac{1}{\sqrt{3}} \left( (-1)^{b_0} \left| 0 \right\rangle + (-1)^{b_1} \left| 1 \right\rangle + (-1)^{b_2} \left| 2 \right\rangle \right). \]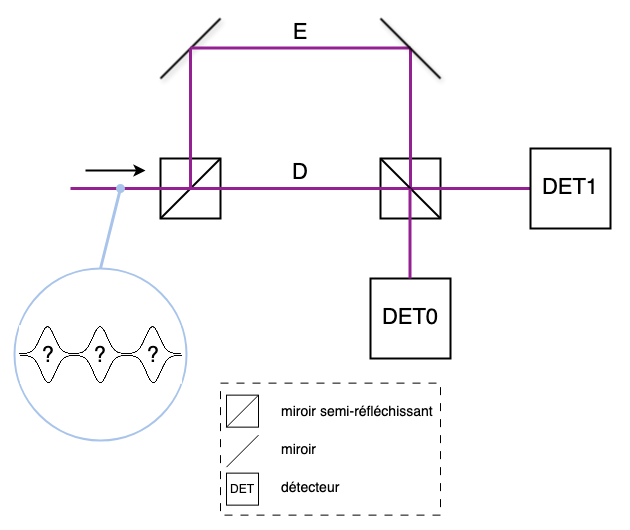
Ici encore, la différence de longueur entre les trajets D et E est telle que le train d'impulsions passant par le trajet E est retardé d'un temps T par rapport au train passant par D. On peut donc représenter les états des trains d'impulsions en entrée du dernier miroir semi-réfléchissant par les états
\[ \left| \psi_D \right\rangle = \frac{1}{\sqrt{3}} \left( (-1)^{b_0} \left| 0 \right\rangle + (-1)^{b_1} \left| 1 \right\rangle + (-1)^{b_2} \left| 2 \right\rangle \right) \]\[ \left| \psi_E \right\rangle = \frac{1}{\sqrt{3}} \left( (-1)^{b_0} \left| 1 \right\rangle + (-1)^{b_1} \left| 2 \right\rangle + (-1)^{b_2} \left| 3 \right\rangle \right) \]Prenons un exemple avec les bits b0 = 0, b1 = 0 et b2 = 1. On aura alors les états suivants
| Impulsion 3 | Impulsion 2 | Impulsion 1 | Impulsion 0 | |
|---|---|---|---|---|
| Trajet D |  |  |  | |
| Trajet E |  |  |  |
Pour deux rayons incidents A et B comme illustré sur la figure suivante,
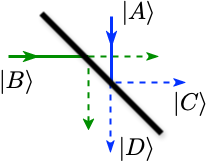
où a, b, c et d sont les amplitudes de probabilité associées aux états \( \left| A \right\rangle \), \( \left| B \right\rangle \), \( \left| C \right\rangle \) et \( \left| D \right\rangle \) respectivement.
On obtient donc \( c = \frac{a + b}{\sqrt{2}} \) et \( d = \frac{a - b}{\sqrt{2}} \).
En prenant les états \( \left| \psi_D \right\rangle \) et \( \left| \psi_E \right\rangle \) décrits précédemment, on peut donc calculer les états qui résultent de l'interférence des impulsions pour chaque temps
| \( \left| \psi_{\text{in}} \right\rangle \) | \( \left| \psi_{\text{out}} \right\rangle \) | |||
|---|---|---|---|---|
| Temps | D | E | DET0 | DET1 |
| T0 | \( (-1)^{b_0} \) | 0 | \( \frac{1}{\sqrt{2}} (-1)^{b_0} \) | \( -\frac{1}{\sqrt{2}} (-1)^{b_0} \) |
| T1 | \( \frac{1}{\sqrt{2}} (-1)^{b_1} \) | \( \frac{1}{\sqrt{2}} (-1)^{b_0} \) | \( \frac{1}{2} ((-1)^{b_0} + (-1)^{b_1}) \) | \( \frac{1}{2} ((-1)^{b_0} - (-1)^{b_1}) \) |
| T2 | \( \frac{1}{\sqrt{2}} (-1)^{b_2} \) | \( \frac{1}{\sqrt{2}} (-1)^{b_1} \) | \( \frac{1}{2} ((-1)^{b_1} + (-1)^{b_2}) \) | \( \frac{1}{2} ((-1)^{b_1} - (-1)^{b_2}) \) |
| T3 | 0 | \( \frac{1}{\sqrt{2}} (-1)^{b_2} \) | \( \frac{1}{\sqrt{2}} (-1)^{b_2} \) | \( \frac{1}{\sqrt{2}} (-1)^{b_2} \) |
On remarque donc que si un photon est mesuré aux temps T0 ou T3, il peut être détecté par le détecteur 0 ou le détecteur 1 avec une probabilité de 50% puisque
\[ \left( \frac{(-1)^{b_0}}{\sqrt{2}} \right)^2 = \left( \frac{-(-1)^{b_0}}{\sqrt{2}} \right)^2 = \left( \frac{(-1)^{b_2}}{\sqrt{2}} \right)^2 = \left( \frac{-(-1)^{b_2}}{\sqrt{2}} \right)^2 = \frac{1}{2}. \]Si le photon est mesuré aux temps T1 ou T2 , les valeurs de \( b_0 \) , \( b_1 \) et \( b_2 \) déterminent le détecteur qui sera activé. Dans le protocole DPS, seuls les photons mesurés aux temps T1 et T2 sont utilisés pour établir la clé, les photons mesurés aux tempsT0 et T3 sont rejetés.
Reprenons notre exemple où \( b_0 = 0,\ b_1 = 0,\ b_2 = 1 \). On a alors les amplitudes de probabilité suivantes :
| \( \left| \psi_{\text{out}} \right\rangle \) | ||
|---|---|---|
| Temps | DET0 | DET1 |
| T1 | 1 | 0 |
| T2 | 0 | -1 |
De façon générale si \( b_0 = b_1 \), (différence de phase de 0) et que le photon est détecté au temps T1, le détecteur 0 est activé et Bob enregistre le bit 0 pour sa clé. À l'inverse, si \( b_0 \neq b_1 \)(différence de phase de \( \pm\pi \)) et que le photon est détecté au temps T1 , le détecteur 1 est activé et Bob enregistre le bit 1 pour sa clé.
Si le photon est plutôt détecté au temps T2 , alors Bob enregistre le bit 0 si \( b_1 = b_2 \) et le bit 1 dans le cas contraire.
Maintenant qu'on sait comment Bob peut établir la clé de chiffrement, il lui reste à communiquer à Alice de l'information qui permettra à cette dernière d'obtenir la même clé, sans toutefois que l'information révélée permette à une personne externe de déduire cette clé.
Tout ce que Bob a à faire, c'est de transmettre à Alice les temps de détection de chacun des photons. Comme on vient de le voir, en connaissant le temps de détection et la valeur des bits b0, b1 et b2 (Alice connait ces valeurs puisque c'est elle qui les a générées), Alice peut savoir quel détecteur a mesuré le photon et donc, la clé de Bob!
Voyons un exemple dans lequel Alice a reçu les temps de détection de 6 photons :
| Photon | b2 | b1 | b0 | Temps de détection | Bit de la clé |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | T0 | – |
| 2 | 0 | 1 | 1 | T2 | 1 |
| 3 | 0 | 0 | 0 | T1 | 0 |
| 4 | 1 | 0 | 1 | T1 | 1 |
| 5 | 0 | 1 | 1 | T3 | – |
| 6 | 1 | 1 | 0 | T2 | 0 |
Les photons 1 et 5 (en gris) sont simplement rejetés car ils ont été détectés aux temps T0 et T3 respectivement. Le photon 2 a été détecté au temps T2, ce sont donc les impulsions modulées par les bits, b1 et b2 qui ont interférées. Puisque la différence de phase est de π entre ces 2 impulsions, Alice enregistre le bit 1 pour sa clé. Pour le photon 3, Bob a annoncé le temps T1, ce sont donc les impulsions modulées par les bits b0 et b1 qui ont interférées. Puisqu'aucun déphasage a été appliqué à ces impulsions, Alice enregistre le bit 0 pour sa clé. Vous pouvez faire l'exercice avec les photons 4 et 6.
Une clé de chiffrement est une information secrète, généralement une suite de bits (0 et 1), partagée uniquement entre deux parties (comme Alice et Bob). Elle permet, grâce à un algorithme cryptographique, de transformer un message lisible (texte clair) en un message chiffré (illisible pour les autres), puis de le déchiffrer. Contrairement à un mot de passe, la clé n'est pas destinée à être mémorisée par un humain, mais à être utilisée par un programme informatique. L'objectif des protocoles comme BB84, E91 ou DPS est de générer et partager cette clé de façon parfaitement sécurisée, afin que seuls Alice et Bob puissent l'utiliser pour protéger leurs communications.
La polarisation décrit l'orientation dans laquelle une onde lumineuse (comme un photon) oscille. Imaginez une corde qui vibre : elle peut le faire verticalement (↕), horizontalement (↔) ou en diagonale (⤢). Pour un photon, la polarisation est une propriété quantique fondamentale qui est mesurée pour obtenir les résultats +1 ou -1.
On dit souvent que tout dans l'univers est composé de particules, même la lumière. Les particules qui composent la lumière sont appelées photons : ce sont les "grains" fondamentaux de l'énergie lumineuse. Dans les protocoles de cryptographie quantique (comme BB84, E91…), les photons servent à transporter l'information entre deux parties. Leur propriété de polarisation permet de coder les bits (0 ou 1), tandis que leur nature quantique garantit la sécurité de la transmission : toute tentative d'interception modifie l'état du photon et peut être détectée.
Un train d'impulsions est une séquence d'impulsions lumineuses (ou d'autres signaux) émises à des intervalles de temps réguliers. En cryptographie quantique, un photon peut être préparé dans un état de superposition de plusieurs impulsions temporelles, formant ainsi un train où l'information est encodée dans la phase relative entre les impulsions.
Une impulsion est une brève émission d'énergie, souvent lumineuse, caractérisée par sa durée, son amplitude et sa phase. En optique quantique, une impulsion correspond à un paquet d'onde de lumière, utilisé pour transmettre de l'information ou interagir avec des dispositifs optiques.
Un miroir semi-réfléchissant (ou séparateur de faisceau) est un composant optique qui divise un faisceau lumineux en deux : une partie est réfléchie, l'autre transmise. Pour un photon unique, le miroir crée une superposition quantique des deux chemins possibles, ce qui est essentiel pour les expériences d'interférence.
La superposition quantique est un principe fondamental de la mécanique quantique selon lequel un système peut être décrit par une combinaison linéaire de plusieurs états propres. Cela signifie que le système n'est pas dans plusieurs états à la fois, mais dans un état unique qui est une combinaison mathématique des états possibles.
Un déphasage est une modification de la phase d'une onde ou d'une impulsion. En optique quantique, un déphasage de π (180°) correspond à une inversion du signe de l'amplitude. Dans le protocole DPS, le déphasage est utilisé pour encoder l'information dans la phase relative des impulsions.
Un interféromètre est un dispositif optique qui sépare un faisceau lumineux en plusieurs chemins, puis les recombine pour produire des interférences. La différence de phase accumulée entre les chemins permet de mesurer des grandeurs physiques avec une grande précision.
Un opérateur unitaire est une transformation linéaire qui conserve la norme des vecteurs d'état dans l'espace de Hilbert. En mécanique quantique, l'évolution d'un système fermé est décrite par un opérateur unitaire, garantissant la conservation de la probabilité totale.
[1] Inoue K, Waks E, Yamamoto Y. "Differential phase shift quantum key distribution." PRL 89.3 (2002): 037902.https://doi.org/10.1103/PhysRevLett.89.037902