Le protocole E91 implique deux acteurs principaux : Alice et Bob, qui jouent des rôles différents. Vous pouvez ici explorer l'ensemble des étapes que chacun d'eux doit suivre pour mener à bien le protocole.
Choisissez de façon aléatoire une base de mesure pour les photons incidents. Notez que chacun des photons que vous recevez forme une paire de Bell avec un autre photon qui est reçu par Bob.
Partagez vos bases de mesure avec Bob.
Extrayez votre clé de chiffrement à partir des résultats de mesure obtenus pour des paires de bases identiques.
Validez votre clé en testant l'inégalité de CHSH avec les mesures effectuées avec les autres combinaisons de bases.
Chiffrez et envoyez votre message à Bob.
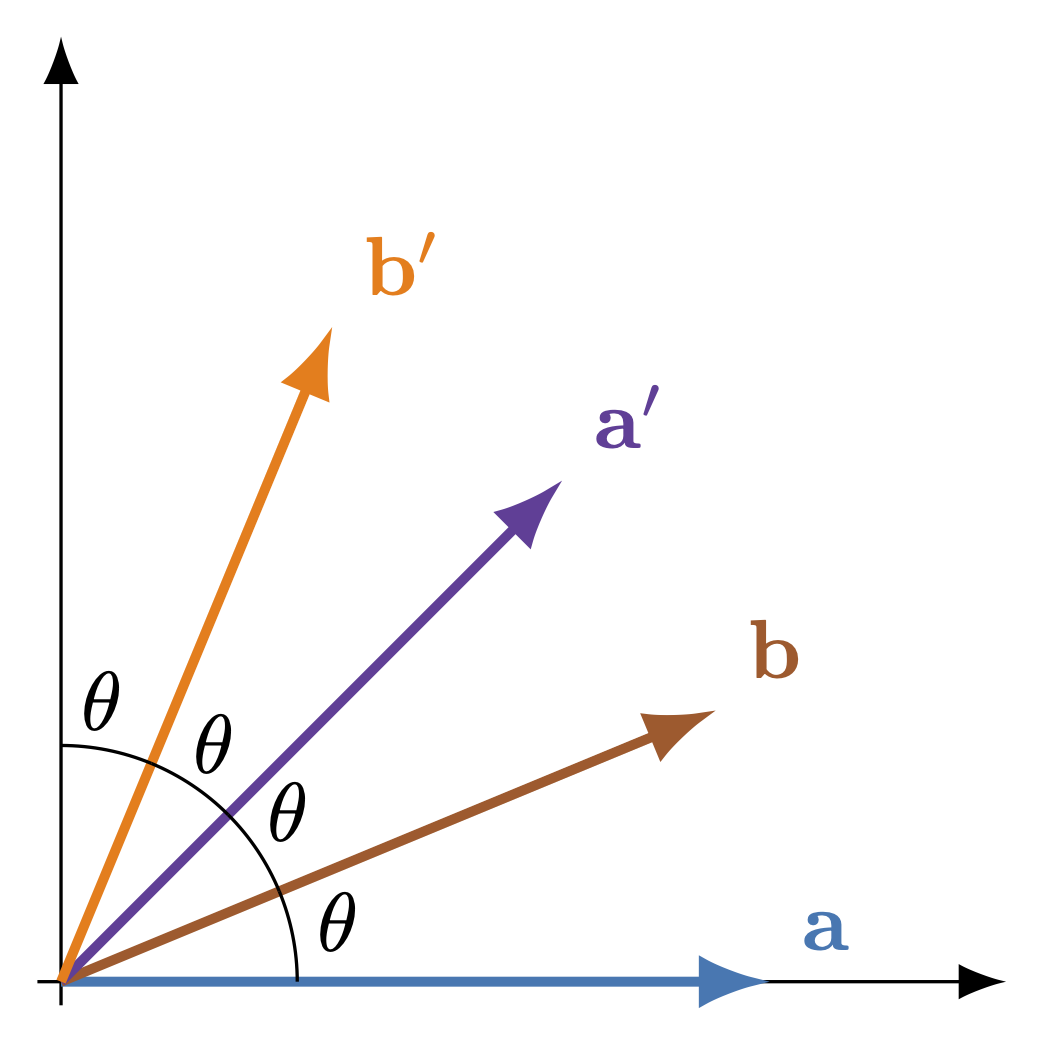
Le protocole a été proposé en 1991 par Artur Ekert[1]. Il implique deux parties distinctes, Alice et Bob, qui souhaitent établir une clé de chiffrement afin de communiquer de manière sécurisée via un canal public. Dans ce protocole, Alice et Bob reçoivent tous les deux un photon provenant d'une source qui émet des paires de photons dont les polarisations sont maximalement intriquées : les photons forment ce qu'on appelle des paires de Bell. Pour chaque paire, la polarisation d'un photon est mesurée par Alice et l'autre par Bob. Alice effectue chaque mesure en choisissant aléatoirement une base parmi l'ensemble de trois bases {a, b, a′}. Bob fait de même en choisissant parmi les bases {b, a′, b′}. Parmi les bases de mesure à leur disposition, Alice et Bob en ont donc 2 qu'ils partagent, b et a′.
Pour chaque mesure, Alice et Bob enregistrent le résultat : +1 ou -1. Une fois la transmission des paires de photons terminée et les mesures effectuées, Alice et Bob divulguent les bases de mesure qu'ils ont utilisées pour chaque photon. Les résultats des mesures effectuées dans la même base sont conservés pour former la clé de chiffrement. Cette situation survient en moyenne 2 fois sur 9 : lorsqu'Alice et Bob mesurent tous les deux dans la base b ou encore dans la base a'. Les résultats des mesures effectuées dans des bases différentes sont révélés et utilisés pour valider la sécurité de la source et du canal quantique qui ont été utilisés. Pour ce faire, le protocole E91 s'appuie une des expériences les plus spectaculaires de la mécanique quantique : la vérification des inégalités de Bell. Il existe plusieurs formulations de ces inégalités et le protocole E91 s'appuie spécifiquement sur l'inégalité de CHSH. Alice et Bob travailleront seulement avec les résultats des mesures effectuées dans les bases suivantes
| Alice | Bob |
|---|---|
| a | b |
| a' | b |
| a | b' |
| a' | b' |
Ce sont donc, en moyenne, 4 paires de photons sur 9 qui sont utilisées pour vérifier l'inégalité de CHSH. Pour chaque paire de résultats issus des combinaisons de bases du tableau précédent, Alice et Bob calculent le produit mA × mB où mA et mB sont les résultats de la mesure effectuée par Alice et Bob respectivement. La moyenne des produits est ensuite calculée pour chacune des combinaisons de base.
En guise d'exemple, supposons qu'Alice et Bob ont effectué les mesures suivantes:
| Alice | Bob | mA × mB | ||
|---|---|---|---|---|
| Base | mA | Base | mB | |
| a | +1 | b | +1 | +1 |
| a | +1 | b | -1 | -1 |
| a | -1 | b | -1 | +1 |
| a′ | +1 | b | +1 | +1 |
| a′ | -1 | b | +1 | -1 |
| a′ | +1 | b′ | +1 | +1 |
Le calcul des moyennes (corrélation E(a,b)) donne :
L'inégalité de CHSH consiste à vérifier que
Il s'avère que lorsque S est calculé à partir de photons intriqués, cette inégalité n'est pas vérifiée. En fait, on peut montrer que 𝑆 = 2√2 ≈ 2.83 pour des photons maximalement intriqués. Ainsi, si l'émetteur de paires de photons est fiable et que le canal de communication n'est pas bruité – ou pire espionné ! – Alice et Bob devraient observer que la valeur de S tend vers 2√2 au fur et à mesure qu'ils augmentent le nombre de paires de photons considérées dans leur calcul. Ils pourront alors utiliser la clé qu'ils ont obtenue pour chiffrer leur message. À l'inverse, si cette valeur demeure sous 2 ils ne peuvent avoir confiance en la clé obtenue et devraient s'abstenir de l'utiliser. Attention, les valeurs moyennes sont des quantités statistiques qui nécessitent un grand échantillon pour être significatives. Pour un nombre limité d'échantillons des anomalies statistiques peuvent survenir et il peut être difficile de tirer des conclusions.
Notez qu'il reste 3 combinaisons de bases de mesure qui ne sont pas utilisées dans le protocole E91 : (a, a'), (b, b'), and (b, a'). Les mesures effectuées avec ces paires de bases sont simplement jetées.
[1] Ekert, A. K. (1991). "Quantum cryptography based on Bell's theorem." Physical Review Letters, 67(6), 661.https://doi.org/10.1103/PhysRevLett.67.661
On dit souvent que tout dans l'univers est composé de particules, même la lumière. Les particules qui composent la lumière sont appelées photons : ce sont les "grains" fondamentaux de l'énergie lumineuse. Dans les protocoles de cryptographie quantique (comme BB84, E91…), les photons servent à transporter l'information entre deux parties. Leur propriété de polarisation permet de coder les bits (0 ou 1), tandis que leur nature quantique garantit la sécurité de la transmission : toute tentative d'interception modifie l'état du photon et peut être détectée.
Une clé de chiffrement est une information secrète, généralement une suite de bits (0 et 1), partagée uniquement entre deux parties (comme Alice et Bob). Elle permet, grâce à un algorithme cryptographique, de transformer un message lisible (texte clair) en un message chiffré (illisible pour les autres), puis de le déchiffrer. Contrairement à un mot de passe, la clé n'est pas destinée à être mémorisée par un humain, mais à être utilisée par un programme informatique. L'objectif des protocoles comme BB84, E91 ou DPS est de générer et partager cette clé de façon parfaitement sécurisée, afin que seuls Alice et Bob puissent l'utiliser pour protéger leurs communications.
Un canal public est un moyen de communication (comme Internet, une fibre optique ou une ligne téléphonique) où toute personne peut potentiellement intercepter ou écouter les messages échangés, un peu comme parler à voix haute dans une pièce pleine de monde. À l'inverse, un canal privé garantit que seuls les interlocuteurs concernés peuvent accéder à la communication, comme une conversation à voix basse à l'écart. Dans la pratique, il est difficile d'assurer la confidentialité d'un canal : c'est pourquoi la cryptographie est utilisée pour rendre les messages incompréhensibles sur un canal public. Dans les protocoles de cryptographie quantique (BB84, E91, DPS…), la sécurité repose sur la physique quantique, et non sur la confidentialité du canal.
La polarisation décrit l'orientation dans laquelle une onde lumineuse (comme un photon) oscille. Imaginez une corde qui vibre : elle peut le faire verticalement (↕), horizontalement (↔) ou en diagonale (⤢). Pour un photon, la polarisation est une propriété quantique fondamentale qui est mesurée pour obtenir les résultats +1 ou -1.
Deux particules (ou qubits) sont dites « intriquées » lorsqu'elles partagent un état quantique commun : leurs résultats de mesure sont corrélés de façon telle qu'il est impossible de les décrire séparément, même à distance. On parle d'« intrication maximale » lorsque la corrélation entre les résultats de mesure est la plus forte possible, c'est-à-dire que les résultats sont parfaitement corrélés ou anticorrélés selon la base choisie (si l'on mesure l'une, on connaît immédiatement le résultat de la mesure de l'autre).
Mathématiquement, un état d'intrication maximale s'écrit sous la forme d'une superposition où chaque résultat possible a la même probabilité : par exemple, pour deux qubits, l'état
signifie que les deux particules sont toujours identiques (00 ou 11), chacune avec une probabilité de 1/2. L'« amplitude » 1/√2 assure cette probabilité égale.
L'intrication maximale est essentielle pour garantir la sécurité des protocoles quantiques : toute tentative d'interception modifie ces corrélations parfaites et peut être détectée.
Les paires de Bell sont des paires de qubits (particules quantiques, comme des photons) préparées dans l'un des quatre états d'intrication quantique maximale, appelés états de Bell. Ces états présentent des corrélations parfaites, impossibles à reproduire avec la physique classique, et sont fondamentaux pour de nombreux protocoles de cryptographie quantique. Les quatre états de Bell sont :
Ils portent le nom du physicien John Stewart Bell. Dans les protocoles comme E91, ces paires assurent la sécurité grâce à l'intrication maximale : toute tentative d'interception altère les corrélations et peut être détectée.
Une base de mesure est un ensemble d'orientations de référence utilisées pour mesurer une propriété quantique, comme la polarisation d'un photon ou l'état d'un qubit. C'est comme choisir l'angle de son « filtre polarisant ». Le résultat de la mesure (par exemple, +1 ou -1, ou bien 0 ou 1) dépend de la base choisie. Dans les protocoles comme BB84 ou E91, Alice et Bob choisissent aléatoirement leurs bases (notées a, b, a′, b′…).
Les inégalités de Bell sont un ensemble de relations mathématiques qui doivent toujours être respectées si la nature obéit aux lois de la physique classique et à l'idée de variables cachées locales (c'est-à-dire que les résultats des mesures sont prédéterminés et aucune information ne voyage plus vite que la lumière). Or, la mécanique quantique prédit – et l'expérience confirme – que certains systèmes intriqués, comme les paires de Bell, peuvent violer ces inégalités : ils présentent des corrélations impossibles à expliquer par une théorie classique. Tester la violation des inégalités de Bell permet donc de prouver l'existence de l'intrication quantique et d'écarter toute explication par des variables cachées locales.
L'inégalité de CHSH (Clauser, Horne, Shimony, Holt) est une version particulière et testable expérimentalement des inégalités de Bell. Elle s'applique à des mesures sur deux qubits intriqués, chacun mesuré selon deux bases différentes. Selon la physique classique, la valeur du paramètre S calculé à partir des corrélations mesurées ne peut pas dépasser 2. Or, la mécanique quantique permet d'atteindre une valeur maximale de 2√2, prouvant ainsi la présence d'intrication et l'absence de variables cachées locales. Dans le protocole E91, la vérification de cette inégalité garantit la sécurité de la clé générée.